Group Lasso regularization

This example solves an inverse problem where the ground truth coefficients (in orange) follow a group structure. In blue are the recovered coefficients for group lasso with different values of the regularization parameter.

The group lasso regularization enters the optimization through its proximal operator, which is implemented in copt through the function prox of object copt.utils.GroupL1().

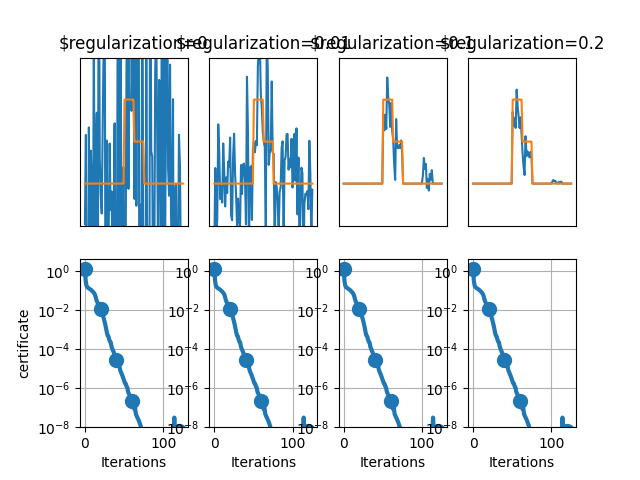
Out:

#features 100
beta = 0
beta = 0.01
beta = 0.1
beta = 0.2

import copt as cp
import matplotlib.pyplot as plt
import numpy as np
from scipy import sparse

import copt.loss
import copt.penalty

np.random.seed(0)

# .. generate some data ..
n_samples, n_features = 100, 100
groups = [np.arange(10 * i, 10 * i + 10) for i in range(10)]

# .. construct a ground truth vector in which ..
# .. group 4 and 5 are nonzero ..
ground_truth = np.zeros(n_features)
ground_truth[groups[4]] = 1
ground_truth[groups[5]] = 0.5

max_iter = 5000
print("#features", n_features)

A = sparse.rand(n_samples, n_features, density=0.2)
sigma = 1.0
b = A.dot(ground_truth) + sigma * np.random.randn(n_samples)

np.random.seed(0)
n_samples = n_features

# .. compute the step-size ..
f = copt.loss.SquareLoss(A, b)
step_size = 1.0 / f.lipschitz

# .. run the solver for different values ..
# .. of the regularization parameter beta ..
all_betas = [0, 1e-2, 1e-1, 0.2]
all_trace_ls, all_trace_nols = [], []
out_img = []
for i, beta in enumerate(all_betas):
    print("beta = %s" % beta)
    G1 = copt.penalty.GroupL1(beta, groups)

    def loss(x):
        return f(x) + G1(x)

    x0 = np.zeros(n_features)
    pgd = cp.minimize_proximal_gradient(
        f.f_grad,
        x0,
        G1.prox,
        jac=True,
        max_iter=max_iter,
        tol=1e-10,
        trace_certificate=True,
    )
    out_img.append(pgd.x)


# .. plot the results ..
fig, ax = plt.subplots(2, 4, sharey=False)
xlim = [0.02, 0.02, 0.1]
markevery = [1000, 1000, 100, 100]
for i, beta in enumerate(all_betas):
    ax[0, i].set_title("regularization=%s" % beta)
    ax[0, i].set_title("$regularization=%s" % beta)
    ax[0, i].plot(out_img[i])
    ax[0, i].plot(ground_truth)
    ax[0, i].set_ylim((-0.5, 1.5))
    ax[0, i].set_xticks(())
    ax[0, i].set_yticks(())

    plot_tos, = ax[1, i].plot(
        pgd.trace_certificate, lw=3, marker="o", markevery=20, markersize=10
    )

    ax[1, i].set_xlabel("Iterations")
    ax[1, i].set_yscale("log")
    ax[1, i].set_ylim((1e-8, None))
    ax[1, i].grid(True)


ax[1, 0].set_ylabel("certificate")
plt.show()

Estimated memory usage: 8 MB